TD5. Séquences de caractères

Le sujet de ce TD est disponible au format pdf ici.

Ce TD a pour objectif de prendre conscience que la notion de complexité a aussi du sens pour l'utilisation mémoire.

Exercice 1 : séquence infinie de caractères

On considère l'analyse d'une séquence de caractères, potentiellement très, très, très longue. On dispose d'une fonction recupere_prochain_caractere() qui renvoie le prochain caractère non traité de la séquence. On considère que le caractère @ indique la fin de la séquence.

On cherche à réaliser un ensemble d'opérations d'analyse sur une séquence donnée. Toutes les opérations doivent être réalisées en une seule passe. Vous devez donc compléter le code suivant afin de réaliser les analyses des questions 1 à 6. Le code que nous rajouterons doit uniquement se situer au niveau des .... Autrement dit, on s'interdit de rajouter du code à l'intérieur de la boucle après la ligne car = recupere_prochain_caractere().

... # initialisation
car = recupere_prochain_caractere()
while car != '@':
    ... # analyse
    car = recupere_prochain_caractere()
... # affichage des résultats

Voici ce que doit être la sortie de notre programme pour la séquence 'a le a    pelle nouveaux 23 15 5  faux fi15n5@' une fois que nous aurons réalisé toutes les opérations des questions 1 à 6 :

a : 4
le : 2
mots : 10
mots finissant par x : 2
moyenne des longueurs des mots : 3.2
somme des nombres: 63

Question 1

 

Ajouter le code nécessaire pour compter les a.

Question 2

 

Ajouter le code nécessaire pour compter les le.

Question 3

 

Ajouter le code nécessaire pour compter les mots. Un mot est une suite de caractères quelconques qui se termine par un ou plusieurs espaces ou par le caractère de fin de séquence @.

Question 4

 

Ajouter le code nécessaire pour compter les mots terminés par x.

Question 5

 

Ajouter le code nécessaire pour calculer la moyenne de la longueur des mots.

Question 6

 

Calculer la somme de tous les nombres de la séquence. Un nombre est l'interprétation en base 10 d'une séquence de chiffres (caractères entre '0' et '9'). Sur l'exemple précédent on obtient ainsi 23 + 15 + 5 + 15 + 5 = 63.

Correction globale

Cliquez ici pour révéler la correction.

#!/usr/bin/env python3
"""Analyse de séquence de caractère"""
def verifier_fin_mot(car_precedent):
    """Doit on rajouter un mot ?

    Renvoie un tuple à 2 éléments :
      - 0 ou 1 indiquant si le mot précédent était vide ou non
      - 0 ou 1 indiquant si le mot précédent finissait par un 'x' ou non
    """
    mot_non_vide = 0
    mots_finissant_x = 0
    if car_precedent != " ":
        mot_non_vide += 1
        if car_precedent == "x":
            mots_finissant_x = 1
    return (mot_non_vide, mots_finissant_x)


def est_chiffre(caractere):
    """Le caractere donne est il un chiffre ?

    Python est un langage de haut niveau : on peut
    comparer directement des chaînes de caractères.
    """
    return "0" <= caractere <= "9"


def main():
    """Point d'entrée du programme"""
    nombre_de_a = 0
    nombre_de_le = 0
    nombre_de_mots = 0
    nombre_de_mots_x = 0
    nombre_courant = 0
    somme_nombres = 0
    somme_longueurs_mots = 0  # = nombre total des caracteres des mots
    car_precedent = " "  # obligatoire (si la sequence est vide
    # ou commence par un espace)

    car = recupere_prochain_caractere()
    while car != "@":
        # On a un caractère qui n'est pas un espace
        if car != " ":
            somme_longueurs_mots += 1
            # a
            if car == "a":
                nombre_de_a += 1
            # le
            if car_precedent == "l" and car == "e":
                nombre_de_le += 1
        # Sinon on vient de finir un mot, éventuellement vide si
        # le caractère précédent était déjà un espace.
        else:
            mot_non_vide, mots_finissant_x = verifier_fin_mot(car_precedent)
            nombre_de_mots += mot_non_vide
            nombre_de_mots_x += mots_finissant_x

        # Gestion des nombres
        if est_chiffre(car):  # Si on est dans un nombre
            nombre_courant = nombre_courant * 10 + int(car)
        elif est_chiffre(car_precedent):  # Si on a terminé un nombre
            somme_nombres += nombre_courant
            nombre_courant = 0

        # On mémorise le dernier caractère puis on passe au suivant
        car_precedent = car
        car = recupere_prochain_caractere()

    # Si le texte se termine par un mot, il faut en tenir compte
    mot_non_vide, mots_finissant_x = verifier_fin_mot(car_precedent)
    nombre_de_mots += mot_non_vide
    nombre_de_mots_x += mots_finissant_x

    # Si il y a un nombre_courant non terminé,
    # c'est à dire que le texte s'est fini par
    # un chiffre
    if nombre_courant:
        somme_nombres += nombre_courant

    # Affichage
    print("a : ", nombre_de_a)
    print("le : ", nombre_de_le)
    print("mots : ", nombre_de_mots)
    print("mots finissant par x : ", nombre_de_mots_x)
    print("moyenne des longueurs des mots :", somme_longueurs_mots / nombre_de_mots)

Exercice 2 : mémoire constante, vraiment ?

Question 1

 

Sommes-nous vraiment certain de ne pas avoir de problème de mémoire ? Pourquoi ?

Correction question 1

Cliquez ici pour révéler la correction.

On peut avoir des problèmes mémoire parce que Python supporte des entiers arbitrairement grands.

Donc les entiers que nous utilisons comme compteurs dans notre programme peuvent devenir arbitrairement grands. Et qui dit entiers arbitrairement grands, dit mémoire arbitrairement grande.

Question 2

 

En supposant que nous puissions traiter un caractère par nanoseconde (1GHz), combien de temps nous faudrait il pour utiliser 1 kilo octet de mémoire avec une séquence ne contenant que des a ?

Correction question 2

Cliquez ici pour révéler la correction.

Nous allons faire ici des calculs "à la louche" pour calculer des ordres de grandeur et donc faire certaines approximations.

Supposons que notre système soit capable de recevoir un caractère par nanoseconde.

Avec une séquence ne contenant que des a on va donc avoir nombre_de_a qui fait + 1 à chaque nanoseconde.

Pour représenter un entier n en mémoire, il faut $\log_2(n) + 1$ bits (et même un peu plus dans les langages haut niveau comme Python).

Donc, pour qu'un entier n utilise 1 kilo octet de mémoire ($= 1000*8$ bits) il faut que n soit égale à $2^{1000*8} + 1$.

Pour que nombre_de_a utilise 1 kilo octet de mémoire, il faut donc $2^{1000*8} + 1$ nanosecondes.

Si on ramène ce nombre en années en divisant par $10^{9} * 3600 * 24 * 365$ on obtient environ $5.5 * 10^{2391}$, soit un bon bout de temps.

Il semblerait que nous soyons tranquilles concernant la mémoire avec notre analyse de séquence.

Question 3

 

Écrire un programme qui sature la mémoire petit à petit de façon visible simplement avec un seul entier.

Correction question 3

Cliquez ici pour révéler la correction.

Nous l'avons vu, il faut grossir beaucoup plus vite qu'en faisant += 1 sur un entier dans une boucle, aussi rapide soit elle. Allons y donc plus fort :

#!/usr/bin/env python3

"""Exemple de code qui sature la mémoire de façon visible avec un entier.

Pour simplifier le programme on fait tout de façon globale, mais nous
sommes conscients que c'est une mauvaise pratique.
"""

import signal

# Ce code est utilisé pour pouvoir sortir
# de la boucle proprement quand ctrl+c est
# tapé au clavier.
ctrl_c_typed = False


def signal_handler(sig, frame):
    print("You pressed Ctrl+C!")
    global ctrl_c_typed
    ctrl_c_typed = True


signal.signal(signal.SIGINT, signal_handler)

print("2^10000 =", 2**10000)
print()
print("computing 2^(2^(n-1)) for n growing 1 by 1 until you press ctrl+c")
print("please LOOK at the memory usage of your machine")

# s(n) = s(n-1) * s(n-1), s(1) = 2 <==> 2^(2^(n-1))
# ça grandit vite, regardons le moniteur système :)
v = 2
count = 1
while not ctrl_c_typed:
    v = v * v
    count = count + 1
    print(count)

print("count =", count)

Comme montré sur l'image ci-dessous, on utilisera le moniteur système de notre système d'exploitation pour voir à quelle vitesse l'utilisation mémoire de notre processus Python grossit. Ici on voit que le processus Python utilise 4,9 GiB de mémoire (il tourne depuis environ 30 secondes).

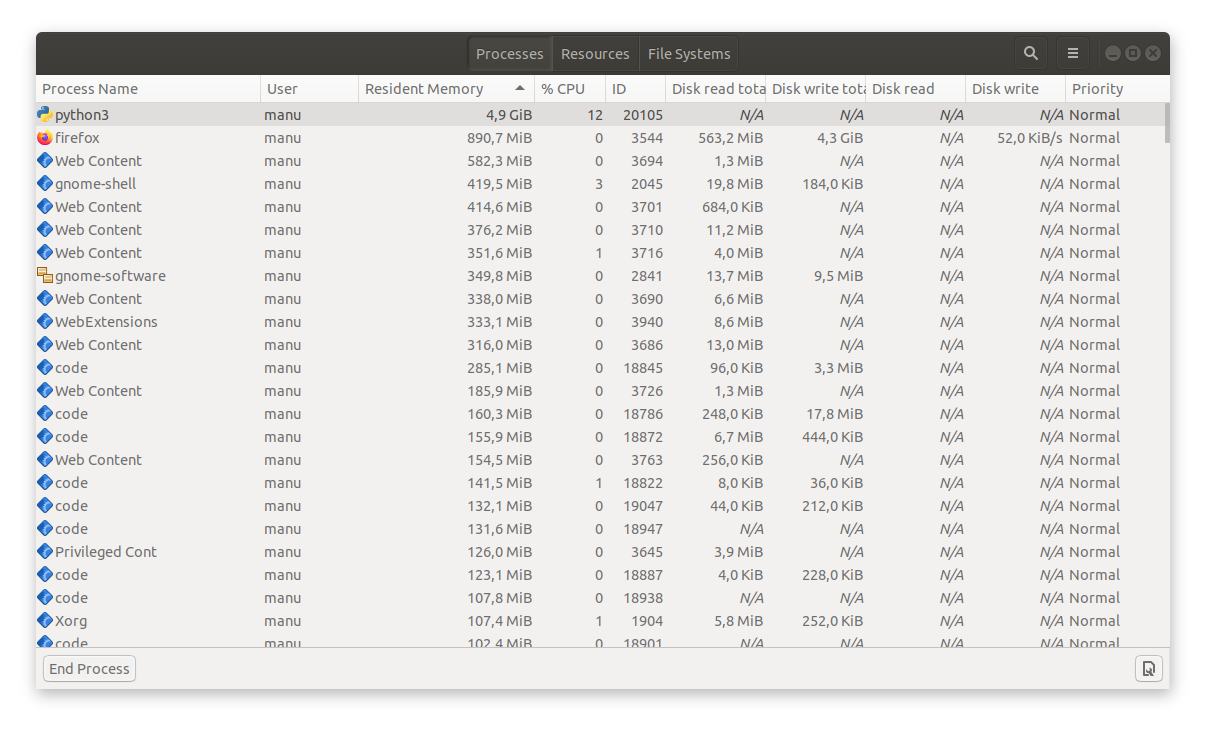
Exercice 3 : mais comment est-ce possible ? (pour aller plus loin)

Question 1

 

Comment l'interpréteur Python fait-il pour avoir des entiers arbitrairement grands alors que sur une machine 64 bits, le processeur supporte les opérations sur les entiers uniquement si ces derniers tiennent sur 64 bits ?